Chapter 5 - Data Analysis - Imaging
Astrometric Uncertainties Point Spread Function
This chapter describes in more detail some of the basic properties of GALEX data.
Astrometric Uncertainties
The positional errors listed in the GALEX photometric catalogs are the errors in the coordinates due simply to counting statistics. For faint sources, these are the dominant source of errors. However, at the bright end, systematic uncertainties in the positions dominant the errors. This section briefly describes the absolute astrometric uncertainties of GALEX data.
We have matched a set of sources from the GALEX GR2 data release of the MIS with objects identified as stars in the SDSS catalogs (type = 6). We have restricted the sample to stars detected in the NUV with aperture magnitudes in the range 17.75 < NUV < 18.25. We only used an NUV-selected sample as the final astrometry for each image in the GALEX pipeline was determined using the positions of stars on the NUV detector. As the astrometric accuracy of the SDSS is about 0.1” even for relatively faint stars, we can consider it essentially an “absolute” reference for our purposes (Pier et al. (2003), AJ, 125, 1559).
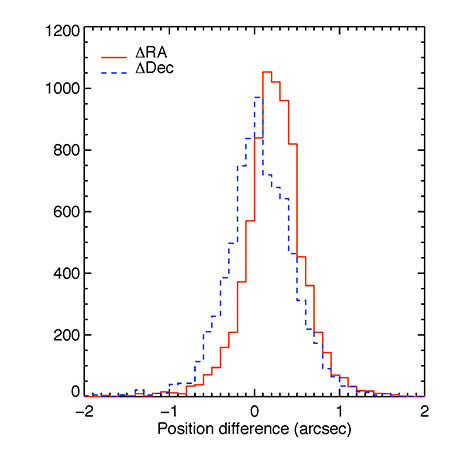
Figure 1 Histogram of the position differences between stars with 17.75 < NUV < 18.25 in GALEX and their positions from the SDSS. The dashed blue line shows the RA difference while the solid red line shows the difference Dec. There is a small overall offset in Dec of 0.2 arcsec while the rms in both coordinates is about 0.4 arcsec.
In Figure 1 we plot histograms of the difference in position in both Dec. and R. A. (multiplied by cos[Dec]) in arcsec in the sense of the GALEX positions minus the SDSS values. There is a small overall offset in Declination of +0.2 arcsec while the one-sigma spread in in each coordinate is about 0.4 arcsec. In Figure 2 we also plot the distribution of radial offsets between the GALEX and SDSS positions. The distribution is fairly consistent with a Gaussian distribution with a sigma of 0.4 arcsec. Similar results were reported in Morrissey et al. (2007) ApJS, 173, 682. who found the absolute positional uncertainty to be 0.5” based upon a sample of QSOs from the SDSS with detections by GALEX.
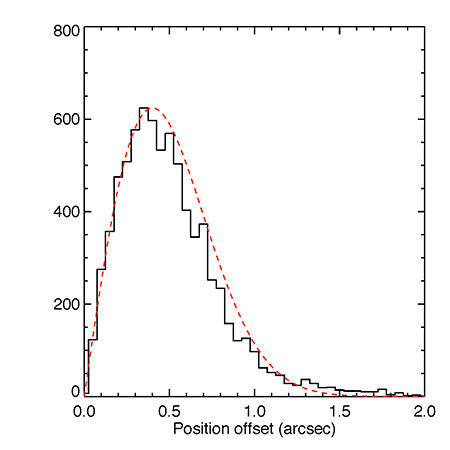
Figure 2 The distribution of radial offsets (solid black line) between the GALEX positions of stars with 17.75 < NUV < 18.25 in GALEX and in the SDSS. The dashed red line is the distribution expected for a Gaussian with a sigma of 0.4 arcsec.
As a routine part of the GALEX pipeline, the astrometry of each field is checked by matching the soruces detected by the GALEX pipeline with positions of known stars. Then these matches are fit with a six parameter plate solution including the RA and Dec of the field center, an x and y plate scale, and an x and y rotation. The best fit values from the plate solution are stored in the file <field_name>-cat_mch_rtastar_stats.txt. After the completion of reprocessing for GR4, it became appartent that there were long term trends in the astrometry of GALEX images with time. These trends from the plate solultions are shown in Figure 3 for MIS fields, where the x and y scales and the x and y rotation angles are plotted as a function of eclipse number ranging across the entire GALEX mission up to the end of December 2007. The x and y pixel scales are gradually increasing with time from about 1.4998 arcsec/pixel at the beginning of the mission to an average of about 1.5005 arcsec/pixel in December 2007. This difference in plate scale from that assumed when constrincting the images corresponds to an average relative position error across the enitre field (1.2 deg) of 0.7 arcsec on average. The average rotation angles have remained constant but the spread has increased with time. These errors in the astrometry have not yet been corrected in either the GALEX images or catalogs. This change in the astrometry may be related to changes in the detector temperature with time. We are planning to fix these trends in the astrometry in future GALEX releases.
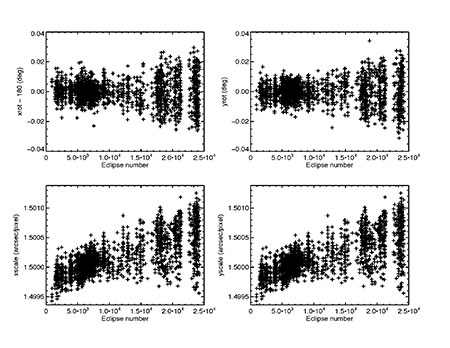
Figure 3 Plots of the x and y plate scale and x and y rotation angels as a function of eclipse number for fields included in the MIS ranging from the beginning of the mission in 2003 up to December 2007. The plate scales have been gradually increasing with time while the spread in rotation angles has also increased. We plan to correct for these long term trends in astrometry in future GALEX releases.
Point Spread Function
We have characterized the GALEX point spread function (PSF) using various in-flight observations. Although the GALEX PSF is in general a complicated function of position on each detector, we begin by characterizing the average PSF in each band.
In order to produce an average PSF, we have relied upon two data sets. The first is a set of field stars while the second relies upon averages of the numerous observations of the primary calibration star LDS 749B. The list of field stars was selected using an SQL search on the MAST CASJobs web sit. We selected all observations of sources that have matches between the GALEX GR2 data release with the SDSS that were classified as point sources from the SDSS pipeline and within a relatively narrow range of UV magnitudes. For the NUV, we selected sources with aperture magnitudes satisfying 16.75 < NUV < 17.25. Due to the lack of bright stars in the FUV, we selected stars in a larger range with 15.75 < FUV < 17.00. These limits insure that the sources are well away from the level where sources become significantly saturated, i.e. for magnitudes NUV < 15.
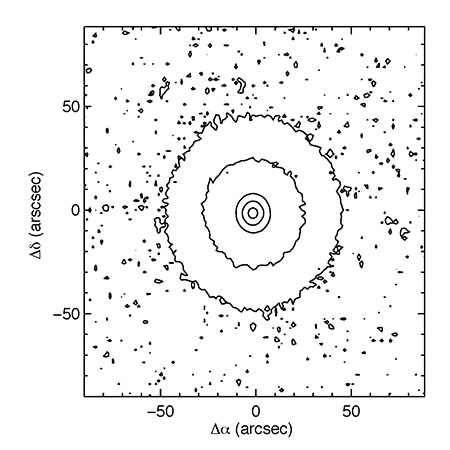
Figure 4 Contour plot of the NUV PSF. The NUV contours range from 5 x 10-5 to 0.5 in steps of a factor of 10. This PSF was genreated by averaging together many point sources from the Medium Imaging Survey in sky coordinates.
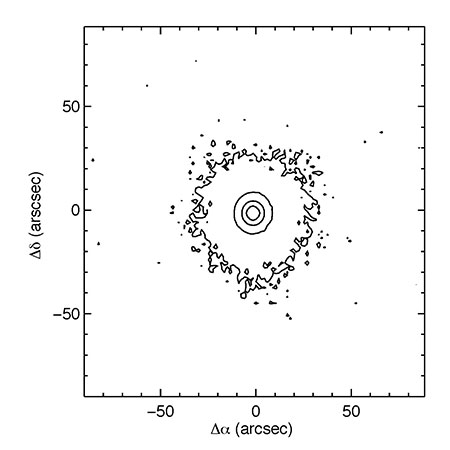
Figure 5 Contour plot of the FUV PSF. The FUV contours range from 2 x 10-4 to 0.2 in steps of a factor of 10. This PSF was generated by averaging together many point sources from the Medium Imaging Survey in sky coordinates.
In each band, we subtracted a local background determined in a circular annulus around each star with an inner radius of 90” and a width of 30”. This background on average is about 3% fainter than the standard GALEX pipeline background in the NUV and about 5% brighter than the pipeline background in the FUV. After subtracting a local background, the profile or each star was scaled to unity total flux. Before stacking the stars together, each individual star was shifted to have it’s center always lie directly on top on a pixel using bilinear interpolation. This prevents the resulting average PSF from blurring just due to sub-pixel shifts in the centroid of each star. Finally, the stars were averaged to gether on pixel by pixel basis using a clipped average. In the NUV, the counts at these magnitudes are large enough such that Gaussian statistics can be used while in the FUV, it was necessary to use the full Poisson distribution, similar to the clipping used in determining the sky background as described in the previous chapter.
Contour plots of the resulting average PSF are shown in Figures 4 and 5 for the NUV and FUV, respectively. Although the GALEX PSFs in general are somewhat elliptical, the PSFs shown in the figures are very axisymmetric since the sources were averaged together in sky coordinates and were selected regardless of their location on the detector. Relative radial profiles for the PSFs in both bands are shown in Figure 6 where the peak of each PSF has been scaled to unity. The PSFs consist of a more or less Gaussian core with extended wings. For the cores of these PSFs the full width half maxima are 4.9” and 4.2” for the NUV and FUV, respectively. The wings of the FUV PSF appear to extend smoothly with radius while the NUV has a “shelf” which extends out to a radius of about 45”, beyond which it falls off more rapidly.
The average PSFs used in these plots can be found in the following two FITS files: PSFnuv_faint.fits (NUV) and PSFfuv.fits (FUV).
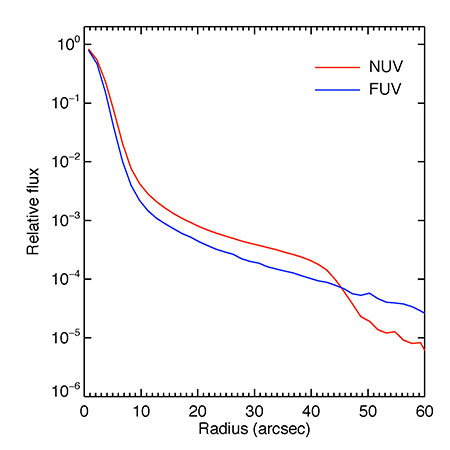
Figure 6 Radial profiles of the FUV (blue) and NUV (red) PSFs.
The corresponding encircled energy curves are shown in Figures 7 and 8 in black for the PSFs generated from the field star sample whereas the dashed red lines show the encircled energy for our primary calibration star LDS 749B from Morrissey et al. (2007). The curves for LDS 749B have the same overall shape as for the field stars although they are a bit broader, particularly in the FUV. This is likely due to two effects. The average for the LDS 749B data does not account for sub-pixel shifts in the centers of each individual observation whereas the field star average does take this into account. A second possibility is that the LDS 749B data are slightly saturated in parts of the detector, particularly in the NUV, leading to a broader encircled energy curve. As is obvious from this section, in order to include all of the light for a given source, a rather large aperture should be used. For faint sources, using a large aperture can greatly increase the error due to sky noise. Often it is advantageous to measure the flux in a smaller aperture and then use an average PSF to compute an aperture correction to account for light lost outside the aperture. We have used the average field star PSF to compute aperture corrections for the radii employed by the GALEX pipeline when computing aperture magnitudes. In Table 1 we list the aperture corrections in magnitudes for the standard GALEX aperture measurements.
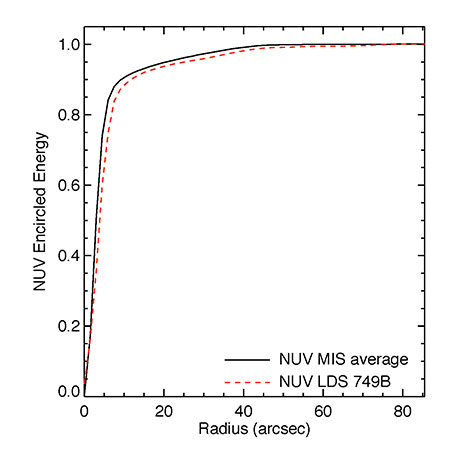
Figure 7 Encircled energy curve for the NUV PSF. The solid black line is the curve for the average field star PSF whereas the corresponding curve for the white dwarf calibration star LDS 749B is shown as the red dashed line.
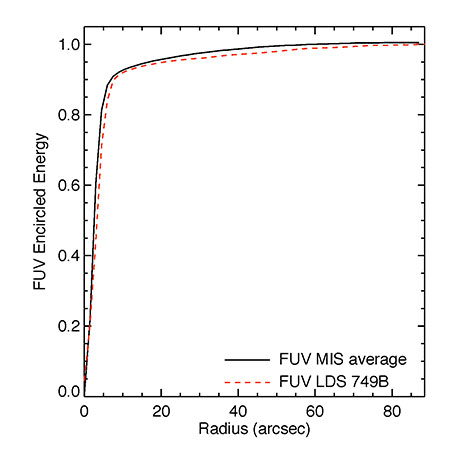
Figure 8 Encircled energy curve for the FUV PSF. The solid black line is the curve for the average field star PSF whereas the corresponding curve for the white dwarf calibration star LDS 749B is shown as the red dashed line.
| Aperture No. | radius (arcsec) | FUV aperutre correction (mag) | NUV aperture correction (mag) |
| 1 | 1.5 | 1.65 | 1.33 |
| 2 | 2.3 | 0.77 | 0.62 |
| 3 | 3.8 | 0.20 | 0.21 |
| 4 | 6.0 | 0.10 | 0.12 |
| 5 | 9.0 | 0.07 | 0.08 |
| 6 | 12.8 | 0.05 | 0.06 |
| 7 | 17.3 | 0.04 | 0.04 |
Since the GALEX PSF varies with position within each detector and in principle from observation to observation, the aperture corrections listed in Table 1 may not apply to a particular observation. If possible, we recommend using bright stars within the image to determine aperture corrections appropriate for that particular image. The PSF tends to become broader near the edge of the field of view. (See Figures 9 and 10 of Morrissey et al. (2007) for more details).




